Основною базою для всіх навчань, пізнають світ, є математика. Точна наука використовує формалізований мову і вивчає порядок, структуру і відносини на обраних абстрактних об'єктах. Не всім учням подобається математика через її складності і заплутаності, а, швидше за все, через нерозуміння. Міцні зміни в ставленні до математики зажадають захопленості, зосередженості, послідовності, навіть впертості і, головне, практичних рішень. У вивченні важливо крок за кроком розбиратися спочатку в простому і поступово переходити до більш складного, не залишаючи незрозумілого і непродуманого.
Існує багато різних розділів математики вже досить вивчених і з'явилися недавно. Далі розповідається про ази математичного аналізу - основних початкових поняттях, визначеннях і правилах дослідження простих функцій однієї змінної, похідної та диференціювання.
У студентів початкових курсів вузів з'явився афоризм: "Математика стає по-справжньому складною, коли з неї пропадають цифри". І дійсно, до розуміння деяких визначень і законів математичної науки наближаються шляхом вирішення за правилами на конкретних прикладах.
Основні визначення
Почнемо з термінології - з простих загальних смислових значень первинних визначень:
- Мінлива - величина або символ, може приймати будь-яке з ряду значень в
певній галузі (вага або зростання дитини)
- функція - призначення, робота, діяльність, певним чином впливати над змінної, позначимо f (x) (залежність ваги дитини від його зростання)
- межа - ліміт, межа, край (горизонт - межа огляду)
- похідна - утворена, вторинна, проістекшая від іншого, позначимо f '(x) (швидкість при русі)
- диференціал - різницю, відмінність, поділ.
Функція це просто
Функція - це результат того, що вона робить зі змінною, що є підсумком обчислення. Це взаємозв'язок елементів, при якій зміна одного змінного обумовлює зміну в іншому. Розділяють f (x) на прості і складні.
Для відображення залежностей використовуються наступні способи: алгебраїчний, графічний, табличний, логічний і навіть програмні.
Визначають числові залежності алгебраїчно з використанням символів змінних, рівності і нерівностей (≤ і>), будується рівняння виду: y = f (x), тут x - змінна або аргумент, а y або f (x) - функція. Кожному конкретному значенню змінної x з допустимої області визначення відповідає певне значення y для заданої f (x).
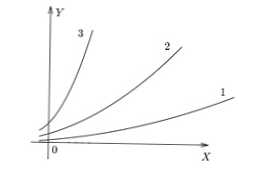
На малюнку нижче представлені прості графіки 3-х різних співвідношень. Видно, що в f (x) 3 виходить найбільше значення y при х конкретному, в f (x) 1 - найменше.
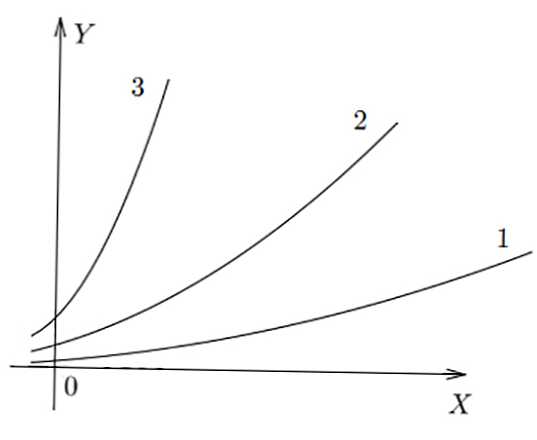
функція
Розрізняють такі елементарні вирази: лінійна (пряма), квадратична (парабола), кубічна, гіпербола, показова, логарифмічна, тригонометричні (наведені в таблиці нижче).
Для аналізу кожного виду f (x) визначають властиві їм властивості (перераховані нижче), для цього використовують поняття похідної і диференціала.
Похідна функції
похідна - оператор, який для початкової f (x) за законами диференціювання ставить у відповідність іншу функцію, вона характеризує зміну первинної f (x) аргументу x в деякій точці. Для її детального розуміння слід розібратися з більш складними визначеннями межі залежності і диференціювання.
межа - це визначення динамічне. Вираз, що x прагне до n, розуміють так - х знаходить значення, які найближче наближаються до п і різняться на мізерну величину.
диференціал - мале зміна якоїсь величини. Приріст назвемо дельтою.
Похідною для f (x) в точці є межа поділу дельти функції до дельті змінної в даній точці, якщо остання прагне до 0.
Характеристика швидкості зміни залежно в даній точці, геометрично її можна показати, як значення tg кута нахилу альфа дотичній до функції.
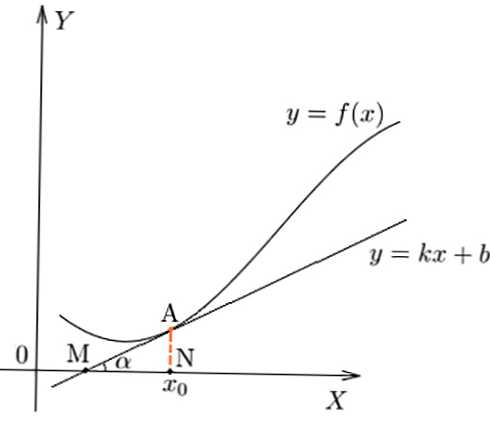
похідна
Залежність називається дифференцируемой, якщо визначена f '(x). Знаходження похідної називається диференціюванням. Правила обчислення f '(x) і відповідності f' (x) від елементарних f (x) наведені в таблиці нижче
Похідна функції також функція
Кожна залежність має певні властивості, знаючи і досліджуючи їх можна аналізувати характер стану і зміни f (x).
Основні властивості:
- Дані проміжків визначень і проміжків значень.
- Нульові значення f (x)
- Функція зростає або убуває в деяких проміжках.
- Точки MAX і MIN функції, чи є перегин.
- Парна або непарна f (x)
- Обмежена і необмежена функція.
- Чи є асимптоти.
- Періодичність f (x).

Функції та похідні
При встановленні характеристик залежності за допомогою похідної використовують взаємозв'язку властивостей f '(x) з властивостями f (x) і навпаки. На графіку функції легко визначаються характеристики f '(x), і навпаки за графіком f' (x) розуміються характеристики первинної f (x). Фіксуючи сутність кожної особливості функції, досліджують і встановлюють ланцюжок зв'язків. Для визначення асимптот в графіках використовують поняття меж.
Нижче наведені деякі характеристики і залежності f '(x) від f (x):
- При зростанні f (x) на проміжку, f '(x) позитивна.
- У разі зменшення f (x) на проміжку, f '(x) негативна.
- При наявності f (x) точки MAX, в ній f '(x) = 0 може не визначена, і tg кута дотичній змінює знак з + на -.
- При наявності f (x) точки MIN, в ній f '(x) = 0 може не визначена, і tg кута дотичній змінює знак з - на +.
- При перегині в Е графіка f (x) значення f '(x) залишилися незмінними в точці знак, f' (x) = 0.
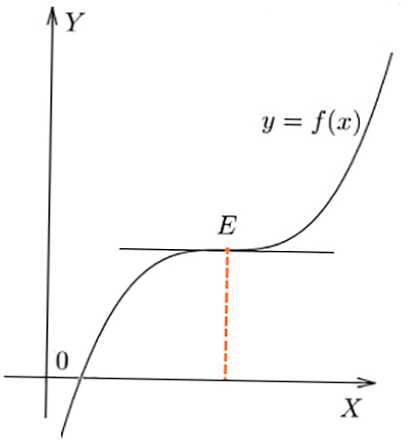
Перегин у точці Е графіка функції
Для дослідження f (x) складають схему, де кожен крок будується за певним алгоритмом обчислень і аналізу взаємозв'язків складових елементів.
Відмінності функції і похідною
Правила додавання і віднімання f (x) однакові з правилами цих дій при диференціюванні. Але правила знаходження f '(x) при діях множення і ділення функцій інші (як в таблиці).
Функція є первинною, а похідна - вироблена вторинна математична операція, у них в більшості випадків різні характеристики.
Крапку перегину безперервної залежності знаходять по її другої похідної, повинен змінюватися її знак в районі точки х0.
Є такі типи функцій не мають f '(x) в точці x0 (розривні). У вираженні ln (| x | -1) не визначена в точці x0 = 1 похідна.
є вирази "По модулю" аналогічні y = | x |, які має злам в х0.
Для подібних залежностей застосовуються лише частково (на проміжках області визначення) способи дослідження їх властивостей за допомогою похідних і не завжди можливий перехід від властивостей f '(x) до властивостей первинної.
Ніде не обійтися без винятків з правил, і навіть в математиці. З метою розбору і закріплення викладеного матеріалу обов'язково слід вирішити приклади, напрактикувалися, набратися досвіду з межами, диференціалами і похідними і сміливо переходити до интегралам.











